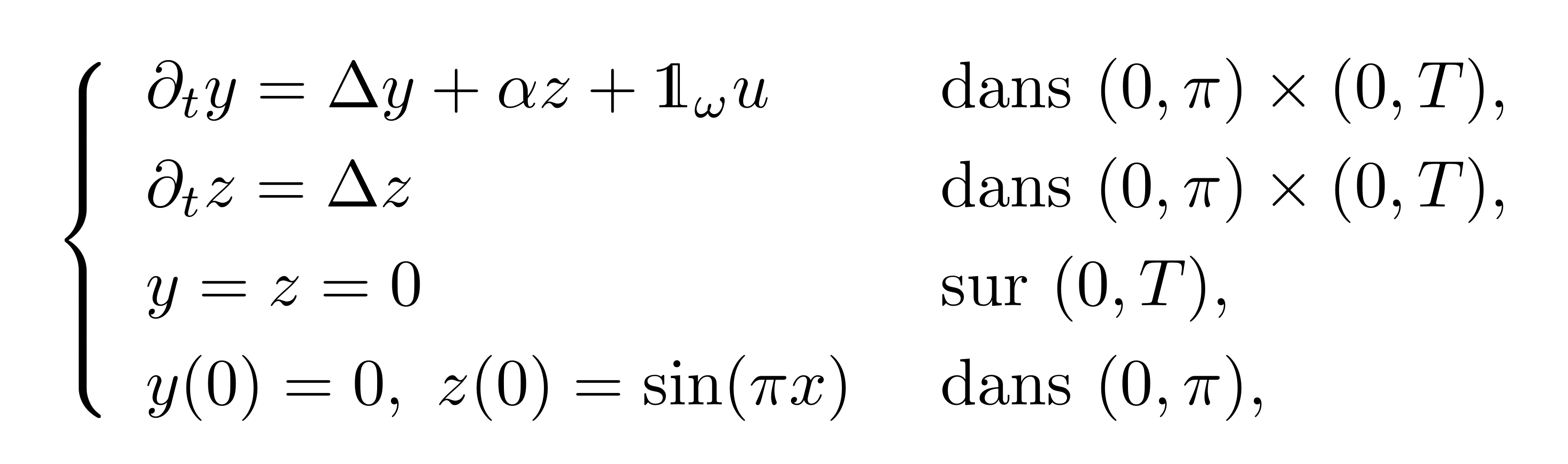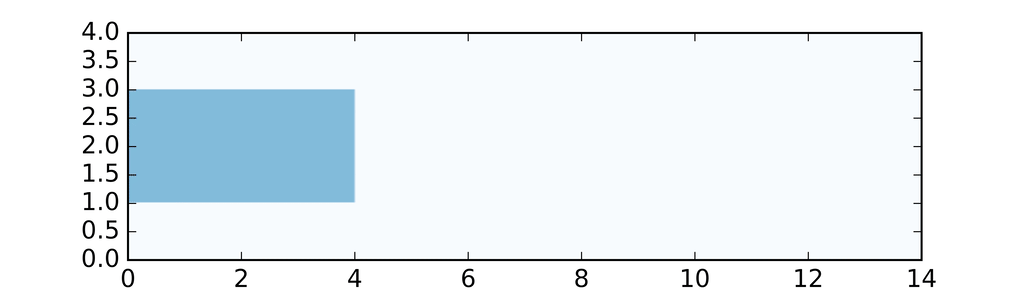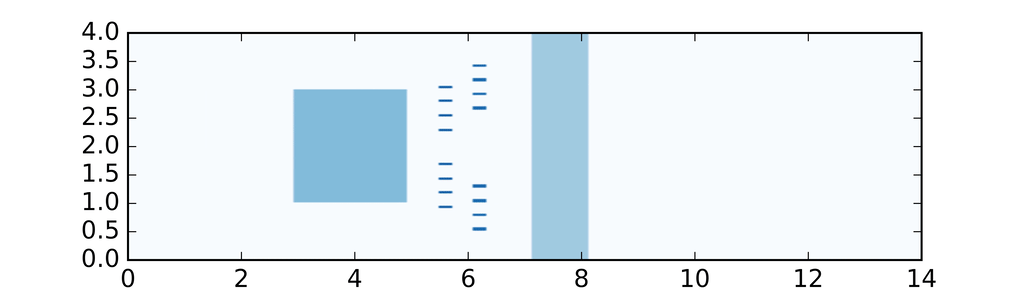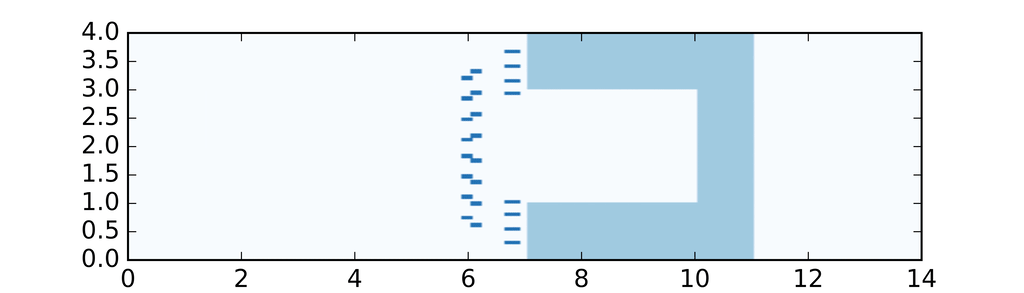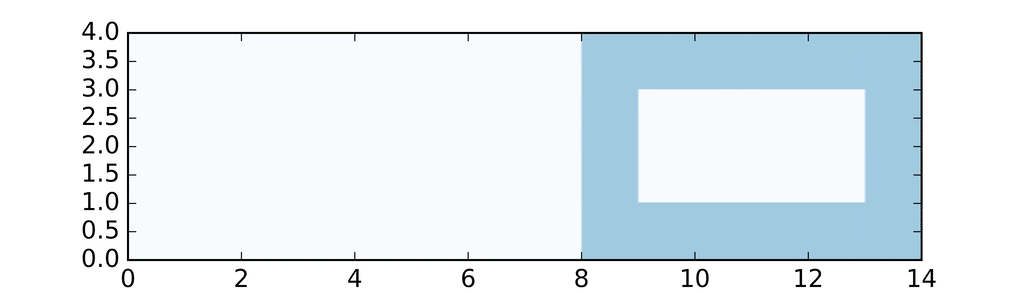
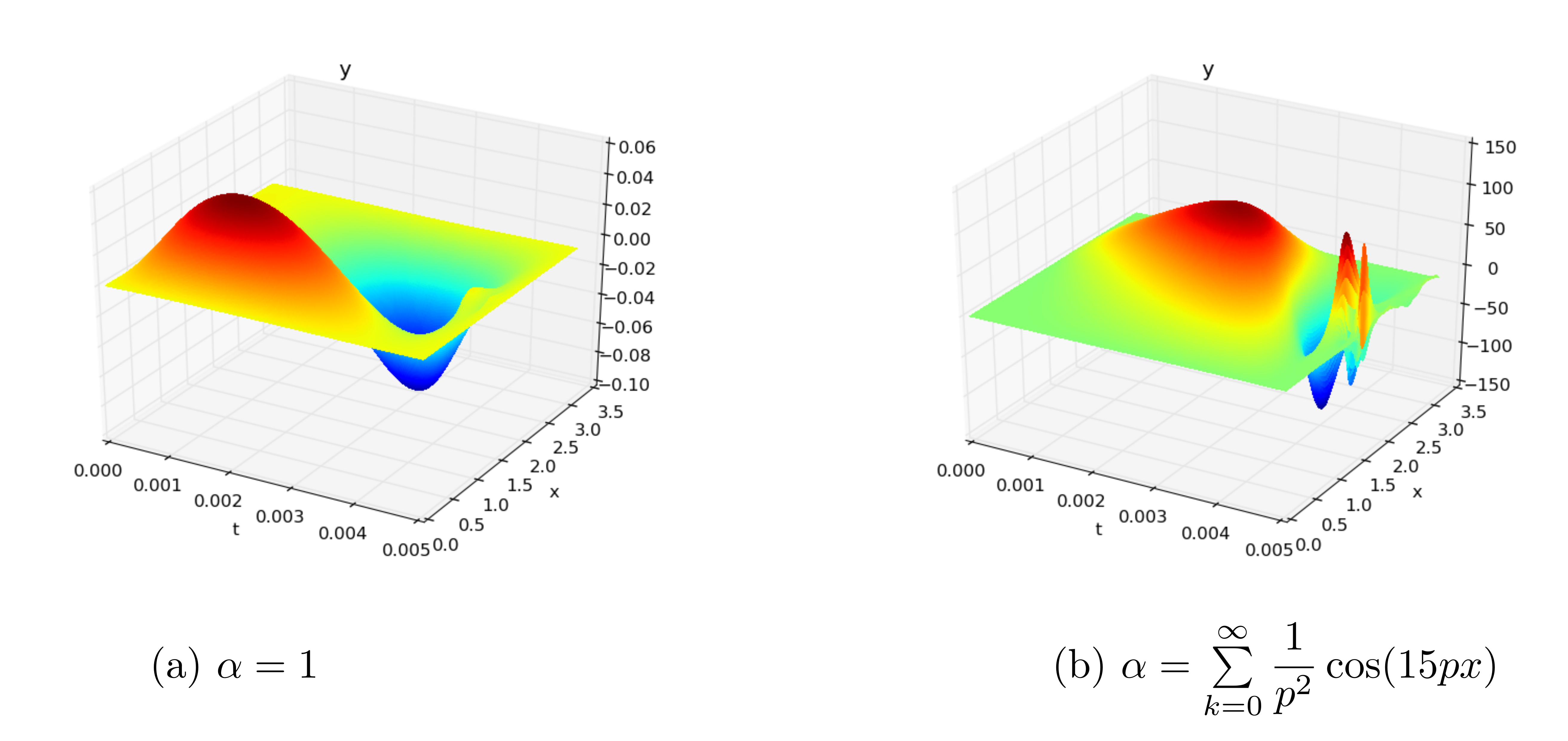
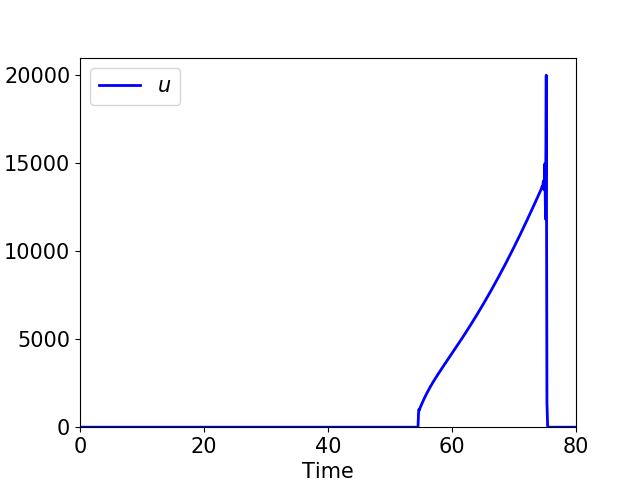
Considérons le système de deux équations paraboliques suivant : pour un coefficient $\alpha$ donné. La question est la suivante : est-il possible de choisir une fonction $u$, appelée contrôle, de sorte que $y(T)$ soit proche (contrôlabilité partielle approchée) ou égale à zéro (contrôlabilité partielle à zéro). Voici ce que l'on obtient dans 2 cas différents : Nous savons que théoriquement dans le cas (a) le système est partiellement contrôlable à zéro, ne l'est pas dans le cas (b), mais est partiellement approximativement contrôlable dans les deux cas. Nous pouvons observer deux phénomènes dans le cas (b) : la norme de la solution expose et de fortes oscillations apparaissent à l'instant $T$.

Code FEniCS sous python : codes (github)

Des techniques biologiques permettent de lutter contre la transmission de maladies telles que la dengue, le zika, le chikungunya... par vecteur des moustiques de type Aedes. La première stratégie, dite Technique par Insectes Stériles (TIS), consiste en des lâchers importants dans la nature de mâles stériles afin de réduire la reproduction des moustiques et par là-même la population totale (Cf e.g. [Anguelov, Dumont, Lubuma 2012] et [Dumont, Tchuenche 2012]). L'objectif est la suppression de la population. La seconde stratégie revient dans ce cas à lâcher des moustiques porteur d'une bactérie appelée Wolbachia bloquant la transmission des virus du moustiques vers l'Homme (Cf e.g. [Hughes, Britton 2013] et [Almeida et al 2018]). Cette fois-ci le but est de remplacer la population présente dans l'environnement.

Dans [A8] en collaboration avec L. Almeida, Y. Privat et N. Vauchelet, nous avons proposer un formalisme mathématique englobant ces deux stratégies à l'aide d'équations différentielles ordinaires modélisant la dynamique des densités de populations des oeufs, des mâles et des femelles. Dans le cas de TIS, nous avons mis en place le modèle suivant

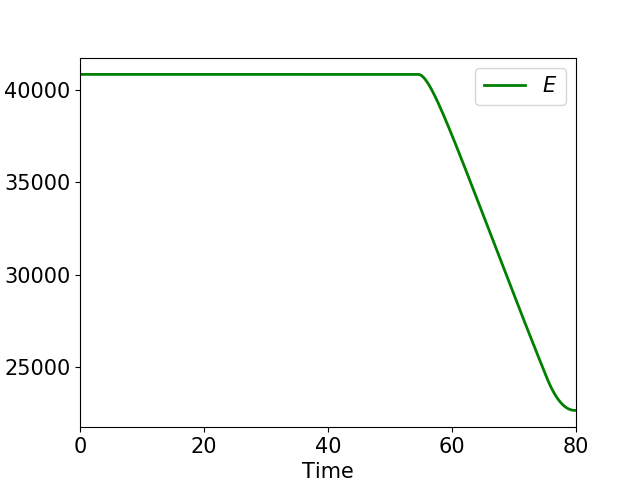
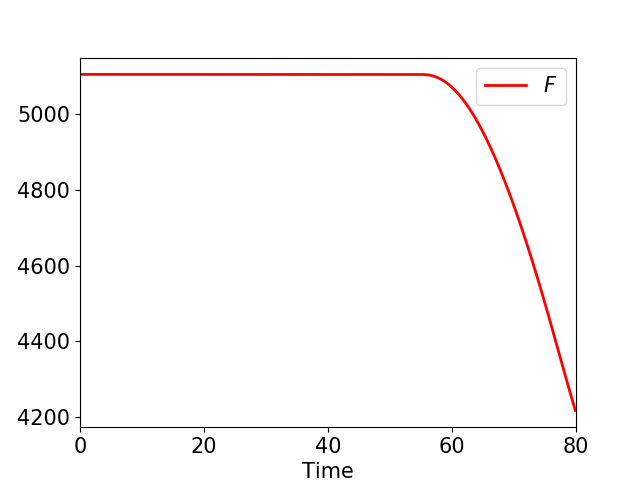
où $E$, $F$, $M$, $M_s$ et $u$ représentent respectivement les oeufs, les femelles sauvages, les mâles sauvages, les mâles stériles présents et les mâles stériles lâchés. Nous avons étudié le problème d'optimisation consistant à minimiser le nombre femelle à la fin de l'expérience pour une quantité donnée de moustiques stériles lâchés. Nous avons montré mathématiquemet par exemple qu'il n'est pas nécessaire d'effectuer des lâchers à la fin de l'expérience. Nous retrouvons ce résultat théorique lors de simulations numériques telles que celles ci-dessous.

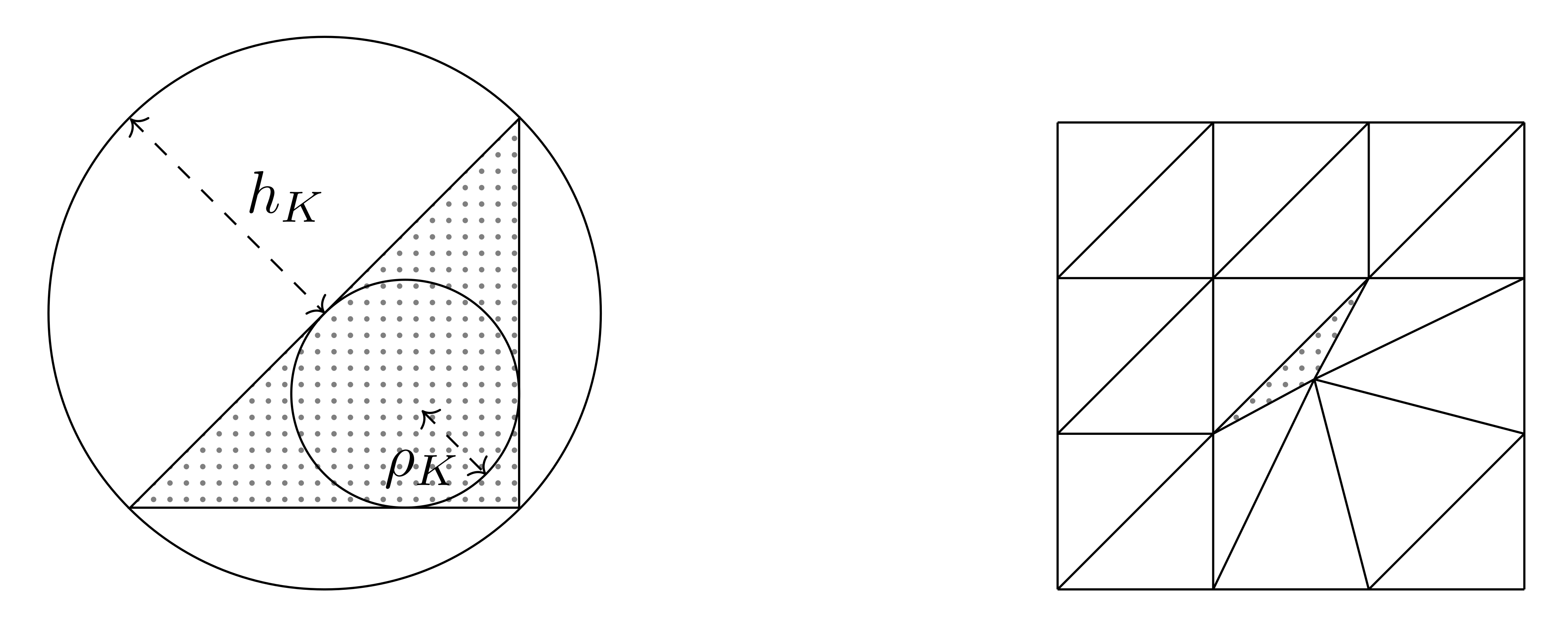
Afin d'assurer une bonne qualité des simulations numériques de type éléments finis, il est bien connu que les maillages utilisés doivent satisfaire certaines conditions géométriques. Si l'on note $u$ et $u_h$ les solutions du problème continu et du problème discret pour un pas de discrétisation de l'ordre de $h$, nous avons, en général (e.g. [Allaire 2012] and [Ern, Guermond 2004]) des estimations d'erreurs dites a priori de la forme

où $h_K$ et $\rho_K$ représentent les rayons des cercles circonscrits et inscrits de la maille $K$ (Cf figure ci-dessous à gauche).

L'estimation précédente devient très mauvaise dès lors qu'une des cellules du maillage est plate comme dans l'exemple donné dans la figure ci-dessus (droite). Certaines études analysent des situations particulières (e.g. [Jamet 76', Babuska & Aziz 76']).

Dans cette étude, nous avons établi des estimations d'erreurs a priori plus précises que l'estimation précédente autorisant des mailles plates isolées en un sens à préciser pour les éléments finis continus de Lagrange sur des problèmes elliptiques. Pour cela, nous avons modifié l'interpolateur de Lagrange continu (e.g. [Erd & Germond 2004], dans le but d'obtenir les inégalités d'interpolation nécessaires aux estimations a priori. Lorsque certaines mailles sont plates, les matrices du système discret que l'on obtient ont un mauvais conditionnement, rendant la résolution de la formulation variationnelle parfois impossible. Afin de pallier cette difficulté, nous utiliserons des méthodes de stabilisation de type Ghost Penalty (e.g. [Burman 2010]).

Code FEniCS sous python : codes (github)

L'impact de la qualité du maillage sur la précision de la solution obtenue par éléments finis peut être quantifié à l'aide d'estimateurs a posteriori. Pourtant, jusqu'à présent, la fiabilité de tels estimateurs d'erreurs pour des problèmes de biomécanique concrets a été peu abordée. Afin d'obtenir des estimations a posteriori sur des schémas de type Galerkine éléments finis, une approche consiste à utiliser des principes de dualité comme pour les études de problèmes de contrôle optimal. Le paradigme alors envisagé est la méthode DWR (Dual Weighted Residuals) qui utilise un argument par dualité pour estimer l'erreur sur une quantité d'intérêt souhaitée (ex. : intégrale de la solution sur une région d'intérêt). De plus, ces estimateurs a posteriori fournissent une stratégie d'adaptation de maillage permettant de diminuer l'erreur numérique de manière significative en augmentant très peu le nombre de cellules du maillage.

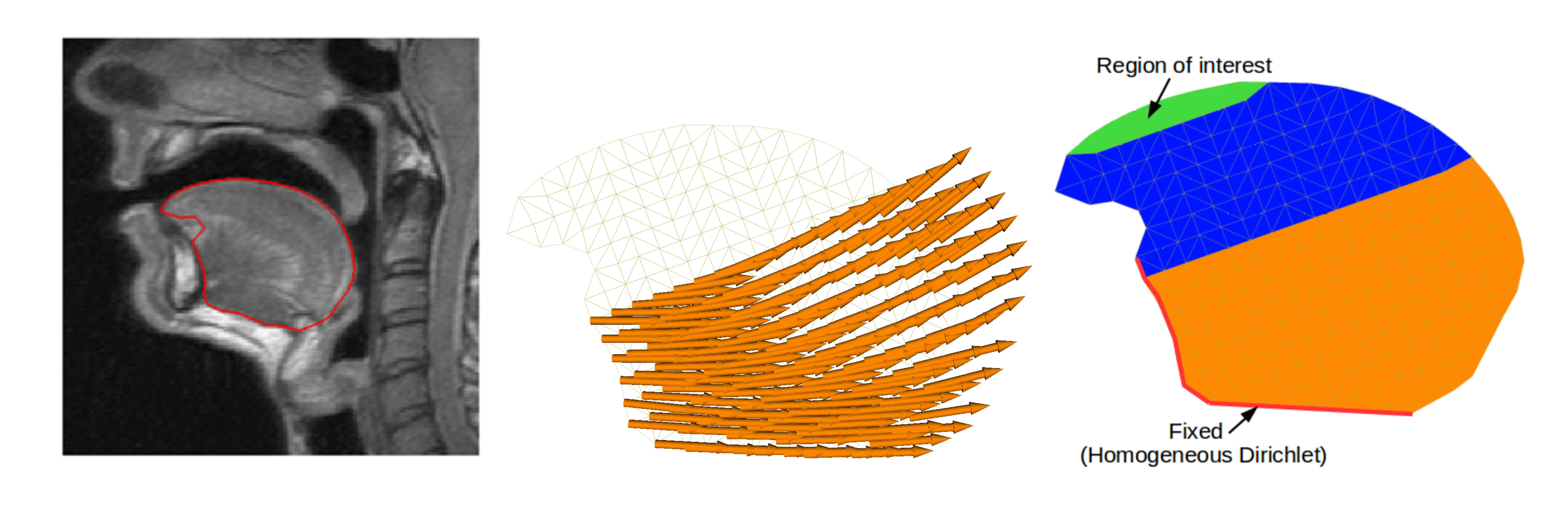
Dans [A10], nous illustrons le fait que ces estimateurs permettent d'assurer la qualité de simulations numériques sur des modèles utilisant des données patient complexes et ayant des propriétés élastiques non-homogènes lorsqu'on cherche à minimiser l'erreur pour une région d'intérêt donnée. Par exemple, nous étudions le déplacement d'une géométrie de langue (figure ci-dessous, gauche) provenant de données patient lors d'une activation musculaire du genio-glossus postérieur (figure ci-dessuo, center) ce qui correspond à la production des phonèmes /i/ ou /s/ et estimons l'erreur numérique commise sur la partie supérieure (figure ci-dessous, droite, région verte).

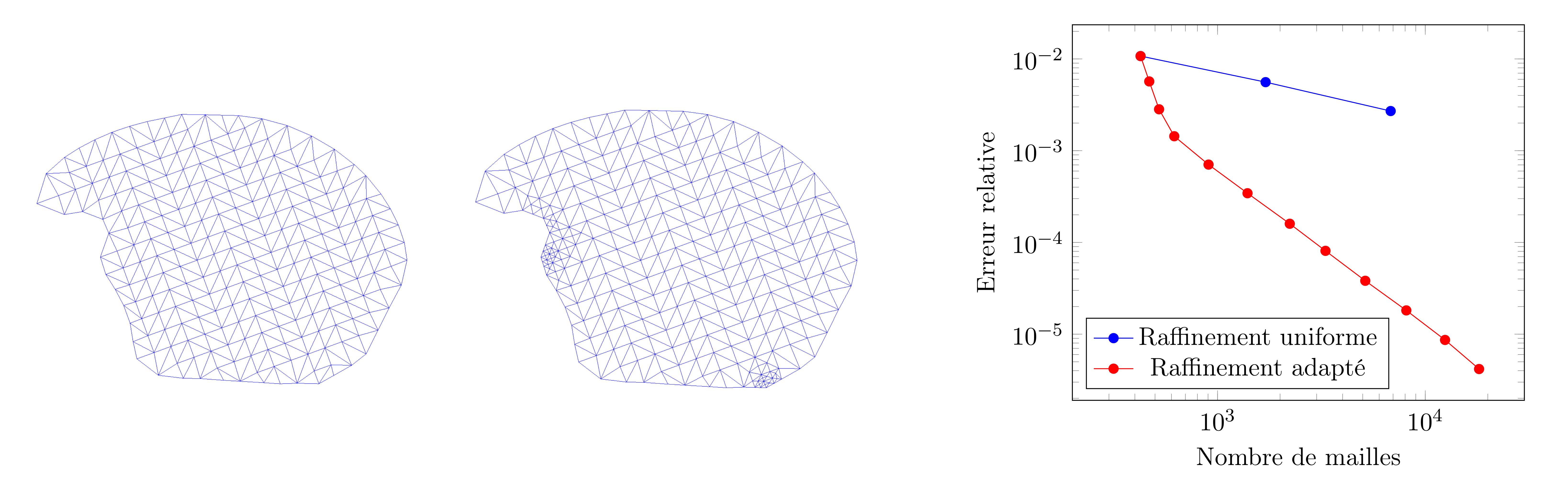
Dans la figure ci-dessous (droite), nous observons qu'après deux itérations de l'algorithme d'adaptation, en ajoutant seulement 97 cellules aux 426 du maillage initiale, l'erreur relative est divisée par trois.

Code FEniCS sous python : codes (github)

Dans [A7,A12], l'objectif a été de construire des commandes de foules en agissant seulement une région donnée de l'espace de sorte à amener une foule dans une configuration finale. Un example est donné dans la figure ci-dessous : la foule initiale μ⁰ (gauche) a une vitesse naturelle v, passe par un domaine ω dans lequel nous autorisons à changer la vitesse des agents et nous souhaitons atteindre une configuration cible μ¹ (droite). Le contrôle u concentre les individus contenus dans les cellules du maillage autour du centre des cellules pour les envoyer au bon endroit.